Now before you run away from a seemingly boring and incredibly technical topic, I want to at least relay the importance of it. Complex financial modeling is at the heart of risk management and dictates how much capital banks, insurance companies, pension funds, corporations, and individuals need to hold in order to meet all of their financial liabilities. This topic is important to understand because it played an integral part in the massive financial destruction that was 2008. I would not be able to write a comprehensive article on financial modeling without approaching the size of a book, but what I will try to do is explain the principal components (no pun intended) of complex financial modeling and why it has to be so complicated.
The first and most important principal in financial valuations is that everything in the financial world is viewed as a stream of cash flows. The only thing that distinguishes between securities is how those cash flows are derived. The simplest type of securities from a valuation perspective are fixed income bonds. A coupon bond has a series of payments each year related to the coupon and one final payment of principal on the final maturity date:
The coupon bond is easy to value because all you have to do is discount the fixed cash flows at current interest rates to come up with the current value. Instruments become difficult to value when their cash flows are unknown and/or variable.
Equity prices can be considered the discounted value of both variable and unknown cash flows. A stock’s value is nothing more than the discounted value of all free cash flows that the company produces from now until infinity (assuming the company survives). Equity analysts spend incredible amounts of time forecasting cash flows and growth rates for individual companies going forward, just so that they can come up with what they believe is a discounted free cash flow “fair value”.
It might have seemed like I went off on a bit of a tangent with simple bonds and equities, but it is important to understand those concepts before we leap into the more complicated. The more complicated items include equity options, mortgage backed securities, collateralized debt obligations, etc. There are many hundreds of ways I can dice up the categories, but nearly every one of them has a common a element – Optionality.
Options, in this definition, make the value of the security depend upon some future observation of a market. I probably lost just about everyone with that statement, but give me a chance to explain. What if I said you needed to value a variable annuity in which the contract provides the policy holder a fixed stream of cash flows 20 years in the future and the size of those cash flows depends upon the level of the S&P 500 in 20 years? This might seem complicated, but in reality this is on the simpler side of options. What if the cash flows did not depend upon the return of the S&P 500 from now until year 20, but instead it was a series of resetting options for 20 years in which every year the gain was locked in and the option was reset? Even better, what if the options depended upon the average performance of multiple indices such as the S&P 500, Eurostoxx 50, and FTSE 100?
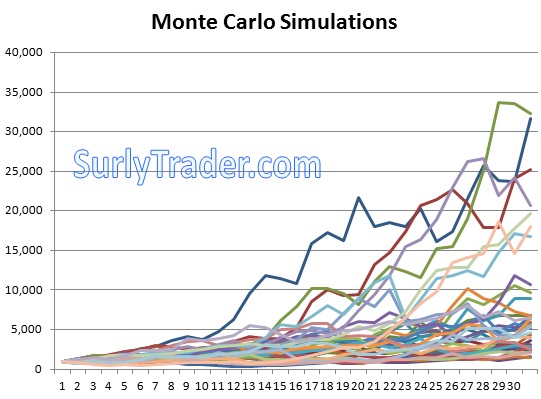
The bottom line is that there is no simple way of valuing complex options. It is not as if there is a simple equation defined for each exotic contract, therefore modern mathematical finance has used “stochastic” processes. A stochastic process is a set of random variables over time. In our case we consider the different markets that we trade in random processes with certain characteristics. By defining these markets as random processes, we can randomly draw an infinite number of paths for each market which allows us to value these “path-dependent options” across all possible market outcomes. As a result, we have a set of valuations across all possible market paths and if we discount all of those valuations to today and average the discounted cash flows we come up with the expected value of this complex option. This simulation process is called a Monte Carlo method.
The above rhetoric might be too much to grasp, but the bottom line is that complex options are valued by looking at the payout over a large number of theoretical market outcomes and then taking the average of those payouts.
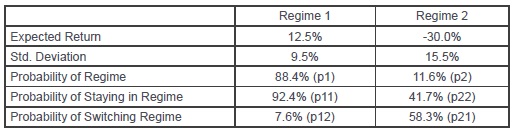
I consider the above monte carlo simulation naive because it simply draws its returns from a normal distribution with mean 8% and standard deviation 20%. With a normal distribution I would never see a return as largely negative as 2008 at about -40%. Therefore there are many refinements that are done to the process to try to account for fat tails. Some have “regime switching” methods in which the model will flip from say an 8% return with 20% standard deviation world to a -10% return 30% standard deviation world. Other models will draw from actual historical observations to account for the actual tail returns.
It is not important to get into the details, but very important to point out some of the flaws. No model is perfect in producing returns that are real world equity returns. Likewise, it is even more difficult to produce random interest rate yield curves that are perfect Now let us take it one step further, how do you create random economic environments that are realistic?
This brings us to the real heart of what we are trying to achieve, and that is a measure of economic capital. How much capital does a firm need in the real world to cover losses under extreme economic environments? This question can only be answered by valuing both assets and liabilities through some sort of monte carlo simulation so that you know what the tail distribution looks for worst case asset/liability ratios. In order to do this, a firm must develop an economic scenario generator. Now we are getting complicated.
An economic scenario generator is just a complex multi-dimensional monte carlo simulation. I explained how important it was to have the correct assumptions and chosen model so that the simulation accounts for fat tails in equity returns, now we not only need fat tailed equity returns, but realistic assumptions for inflation, credit spread movement, interest rate curves and the correlations and interactions amongst all of these factors. Now you can see that the sort of difficult problem just became extremely difficult. This is an area of finance that is under heavy development but still in its infancy.
This complexity should segue into the bank failures during this last credit crisis. How could their models not have told them that the risks on their balance sheets were too much for the capital that they held? The answer is multi-faceted with reasons stemming from compensation plans to stockholder interests, but on the financial risk modeling side it was simple: they did not model it completely and if they thought they were modeling it well they either did not believe it or did a shoddy job of modeling. The underlying instruments such as the highly leveraged CDO’s were complicated enough to value by themselves, but when you put the whole mess together it was even more hopeless.
The positive spin is that 2008 has provided real world extreme market conditions that show just how terrible things can get. Previous to 2008, all financial companies relied upon rather muted historic data to “stress test” their balance sheets. In retrospect, we all know that using historic data did not show them the extreme stress test that these financial institutions would endure during 2008. Going forward, the banks will be sure to run their “2008 Scenario” first and foremost to test the strength of their balance sheets.
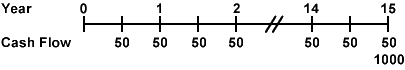









Comments
Sol Nasisi
December 12, 2009
It seems the banks forgot the term "past results do not guarantee future performance." It also seems that banks couldn't see the forest through the trees. Nothing goes up forever and usually the magnitude of the drop is related to the climb. It was inevitable that housing was going to come down. Did they not expect this or just thought they had enough capital to weather a real estate downturn?
Is this review helpful? Yes:0 / No: 0
surlytrader
December 12, 2009
Or was it possible that a lot of the people involved in making profits from the rising housing market did not really care if the market tanked? The biggest fault in bank risk management during the credit crisis was the lack of repercussions and clawbacks for poor lending practices. If you get a bonus every year based upon rising revenue and your worst case situation is to find yourself unemployed and having to find another job what do you do? You keep trying to get large bonuses as long as you can.
And on a grander scale, what about the banks themselves? How many actually went bankrupt and bust due to their terrible lending practices? Washington Mutual, Countrywide, Wachovia, Merrill....but even then, they were fed soft landings via taxpayer subsidized mergers.
Is this review helpful? Yes:0 / No: 0
Add your Comment
use your Google account
or use your BestCashCow account